|
Analysis of the Economic Impact of the US-Australia Free Trade Agreement ―Focusing on Agricultural Issues― |
|
2. Analysis of Trade Liberalization Negotiations, Based on Bargaining Theory 3. US-Australia Free Trade Agreement |
|||||||||||||||||||
|
2. Analysis of Trade Liberalization Negotiations, Based on Bargaining Theory (1) Analysis of Tariff Competition Riezman [8] applied the combined analysis framework of a non-cooperative game and a cooperative game to the analysis of tariff competitions with tariff negotiation and without. First, a tariff competition is explained in a framework of non-cooperative competition. A presumed situation is expressed by a strategic game. Each of the two countries in the game has a strategy to keep current import tariff rates and a strategy to remove its tariff barrier. The set of strategies each player can opt for is designated as "Set S". Each country has two strategies. Therefore, S 1 ={1,2} and S 2 ={1,2} . When the first country employs strategy i and the second takes strategy j, the first country's profit is designated as "aij" and the second as "bij". This game is then expressed as a profit matrix, as shown below; where a11 > a21, a12 > a22 and b11 > b21, b12 > b22. Temporary values are given in this game as shown in Table 1.
Each player anticipates the strategy to be taken by the other player and opts for a strategy that will maximize his own profit based on such anticipation. This is called an optimal solution. When a strategy selected by a player is the optimal solution to the other party’s strategy with respect to both players, the combination of these strategies is called the Nash equilibrium. When each player adopts strategy
s 1 f
i ( s*)
Assuming a profit matrix of the tariff competition game as given in Table 1 above, the Nash equilibrium is the "maintenance of the tariff" for both countries. Firstly, if the first country opts for "tariff elimination", the second country can obtain a higher profit by "maintaining the tariff". However, when the second country opts for the "maintenance of the tariff", the first country can obtain a higher profit by "maintaining the tariff". When the first country changes its strategy to the "maintenance of the tariff", the second country can obtain a higher profit by "maintaining the tariff" than by taking any other strategy, so that the second country does not change its strategy. When both countries take the strategy of "maintaining the tariff", there will be no incentive for each party to change its strategy. This is the Nash equilibrium formed in a tariff competition. However, the Nash equilibrium is not the best combination of possible and desirable strategies. As a party is able to increase its own profit from the Nash equilibrium without damaging the other party's profit, the Nash equilibrium is not Pareto optimal. In other words, both parties can increase profits above the Nash equilibrium when both parties take the strategy of "tariff elimination". In a tariff competition, the result of each party's reasonable policy option will not be reasonable as a whole. This is called unsatisfied common rationality. In order that both parties pursue profit higher than the Nash equilibrium, it is necessary to introduce negotiation. (2) Analysis of Tariff Negotiation Next examined is the case where the parties will cooperate for the purpose of increasing their own profits, or a negotiation case (1). First it is necessary that both parties are always able to win more profit through negotiation than the non-negotiation case. Otherwise, neither party has any motive to start negotiation. This is called the assumption of individual rationality. Profit obtained without negotiation is called the reference point of negotiation d = (d 1, d 2) (2). Here, based on Table 1, the reference point of negotiation is deemed to be the Nash equilibrium where both countries "maintain the tariff". Starting from this point, both countries set out to negotiate to seek further profits. The non-cooperative game was a definitive analysis (3) composed of two strategies for each party and four conclusions. Now a statistical concept is introduced to single out one conclusion from the four. This is called the concept of mixed strategy. Each of the four conclusions is given a probability of occurrence as follows;=
The method of determining in correlation with each other's option is called a correlated mixed strategy. Each player must negotiate in order to increase his own expected profit. By setting up as above, a set of realizable expected profits can be determined. This set is called a realizable negotiation set U. A vector in U of expected profits realizable through cooperation is expressed as u = (u 1, u 2 ). Besides, the expected profit realizable through negotiation shall satisfy the condition of individual rationality. Therefore, ui
> di , i = 1,2 ,
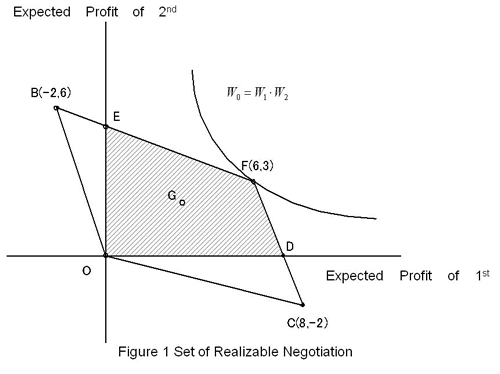
d When a set of realizable negotiation is charted, based on Table 1, Figure 1 is drawn. The origin O is made the reference point of negotiation d. The reference point represents the expected profit obtained by both countries when taking the strategy of "maintaining the tariff". Negotiation will not be agreed upon unless expected to increase profit further. Therefore, Point B, realized only when the first country selects the strategy of "maintaining the tariff" and the second country opts for the strategy of "tariff elimination", or its opposite point C is excluded from negotiation. To be negotiated is the region above the point of reference O in the set of realizable negotiation. The shaded area OEFD in Figure 1 represents that region. Point F represents the expected profit obtained when both countries opt for "tariff elimination" at 100% probability.
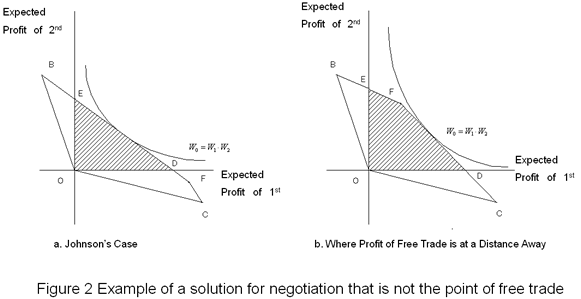
In the region of negotiation any random point on EFD is Pareto optimal. For example, the point of negotiation conclusion is assumed to be point G in the shadowed region. Point G represents increased profit for both countries, being in the shadowed region. But negotiation continues for further profit increase, because negotiation makes it possible for both countries to increase expected profit of the first country without decreasing expected profit of the second country realized at point G. Conversely it is possible to increase the profit of the second country without decreasing the first country's. At point G Pareto optimum is not satisfied, and there remains room for negotiation to increase expected profits mutually. On EFD, however, it is not possible to increase one party's profit without sacrificing the expected profit of the other party, so that Pareto optimum is satisfied. Now the expected profit that is added to the profit at the point of reference is expressed as (3) Free Trade Being No Solution of Negotiation In the course of FTA negotiation, an agreement, short of perfect free trade, is often reached incidentally through compromise, by excluding exceptional commodities or establishing a long transition period until tariff elimination. Such a compromise could be theoretically affirmed, because it is required that some conditions are satisfied in order to conclude a negotiation for perfect tariff elimination. Two examples demonstrating that a negotiated solution is not free trade with perfect tariff elimination are shown (Figure 2). Figure 2 (a) illustrates a situation where the second country can only earn profit below the point of reference in free trade. As Point F is located in the 3rd quadrant, free trade is out of the region where free trade is negotiable. In other words, free trade does not satisfy the condition of individual rationality, so that it is not negotiated. This kind of case is called "Johnson's case".
In Figure 2 (b) it is indicated that free trade may not become a solution of negotiation, even if it satisfies the condition of individual rationality and is found in the quadrant where it is negotiable. Point F is located in the first quadrant, satisfying the condition of individual rationality for both countries, but Curve W0 does not contact Point F, so that Point F is not chosen as a solution of negotiation. Let us consider the condition that free trade becomes a solution of negotiation. Point B was expected profit when the second country eliminated tariffs and the first country maintained its tariff system. On the other hand, Point F was expected profit when both countries eliminated tariffs. The inclination of BF is equal to (Increment to the second country's expected profit)/(Decrease in the first country's expected profit) when shifting from Point F to Point B. Meanwhile, Point C is expected profit when the first country eliminates tariffs and the second country maintains tariffs. Therefore, the inclination of Slope CF is equal to (Decrease in the second country's expected profit)/(Increment to the first country's profit) when shifting from Point F to Point C. After all, Point F contacts W0 when the inclination of Point F and the tangent to Curve W0 is greater than the inclination of BF and smaller than the inclination of CF. The inclination of Point F and the tangent to Curve W0 (W1, W2 ) is W2 / W1. In the meantime, the inclination of BF equals (b21 - b11)/(a11 - a21) according to Equation (1) and that of CF equals (b11 - b12)/(a12 - a11). From the foregoing discussion, the condition required to select Point F, which represents free trade, is,
Incidentally, if the profits of both countries are equal at Point F, the condition of the above expression is apparently satisfied and free trade is always chosen as a solution of negotiation.
|
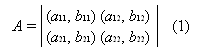

 S
S s
i
s
i  0,
0,